Benchmarks
This page provides the benchmark results for two multimodals problems, running in two different constraints setup and with both ILS and HC algorithms.
Benchmark 1
This benchmark problem uses the Meta.Functions.example_one function, also shown in the image below.
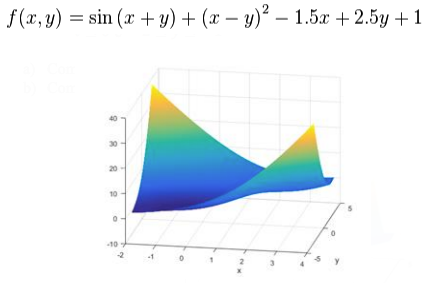
30 individual runs was executed under two different setups: Configuration 1.a with more relaxed variable constraints and Configuration 1.b with a less relaxed constraints.
Configuration 1.a
This setting had the following constraints on variables:
- −1.5 ≤ 𝑥 ≤ 4
- −3 ≤ 𝑦 ≤ 4
Hill Climbing Parameters
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 50
Iterated Local Search Parameters
- Perturbation size (step size): 0.5
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 50
- Local search algorithm: Hill Climbing, with:
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 2
Results and Discussion
The 30 independent individual executions results ran is shown in the table below:
| Algorithm | Minimum | Maximum | Mean Average | Std. Deviation |
|---|---|---|---|---|
| HC | -1.913115 | 1.240485 | -0.264049 | 1.436836 |
| ILS | -1.910092 | 1.510261 | 0.433561 | 1.215818 |
The boxplot for both executions is also shown in the image below:
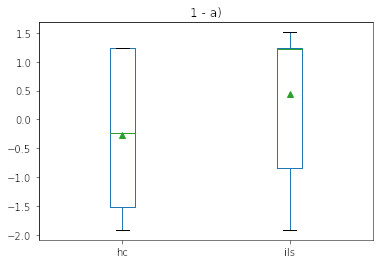
The results shows a good overall performance by HC since it's variety is not as good as the ILS. Since the ILS algorithms tends to change its attraction roundabouts, the mean average its way poorer, but the minum value found, hence the best overall result, is better than the one found in the HC. For overall experience of the author, these stats is not the preferable choices, since the random pattern behaviour of both approaches tends to have outliers that never leaves its local minimums/maximums. A good statistical choice would be the median and/or the median average deviation instead of the mean and standard deivation.
The results overall, are expected, but a little too far off the mean average for ILS, which suggests a perturbation size not optimal, that was choice empiracally and not changed for academic results.
Configuration 1.b
This setting had the following constraints on variables:
- −1 ≤ 𝑥 ≤ 0
- −2 ≤ 𝑦 ≤ 1
Hill Climbing Parameters
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 50
Iterated Local Search Parameters
- Perturbation size (step size): 0.5
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 50
- Local search algorithm: Hill Climbing, with:
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 2
Results and Discussion
The 30 independent individual executions results ran is shown in the table below:
| Algorithm | Minimum | Maximum | Mean Average | Std. Deviation |
|---|---|---|---|---|
| HC | -1.913168 | -1.906510 | -1.912136 | 0.001312 |
| ILS | -1.913215 | -1.910281 | -1.912661 | 0.000619 |
The boxplot for both executions is also shown in the image below:
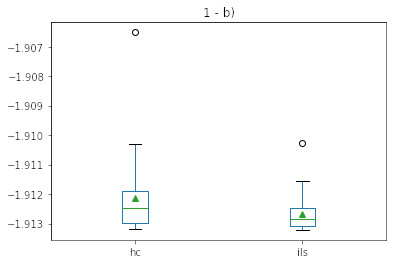
The results shows a better mean average, minimum and maximum result for ILS as it's expected, since the randomness is reduced in a smaller search space and also tends to converge faster in a more robust environment. Nothing too particular to note here, just that ILS is a better approach towards these kind of algorithms than HC alone, as we can see in the results table and boxplot.
Benchmark 2
This benchmark problem uses the Meta.Functions.example_two function, also shown in the image below.
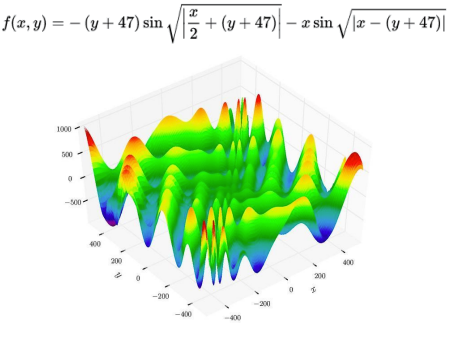
30 individual runs was executed under two different setups: Configuration 2.a with more relaxed variable constraints and Configuration 2.b with a less relaxed constraints.
Configuration 2.a
This setting had the following constraints on variables:
- −512 ≤ 𝑥 ≤ 512
- −512 ≤ 𝑦 ≤ 512
Hill Climbing Parameters
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 500
- Max consecutive iterations without improvements allowed: 50
Iterated Local Search Parameters
- Perturbation size (step size): 0.5
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 50
- Local search algorithm: Hill Climbing, with:
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 2
Results and Discussion
The 30 independent individual executions results ran is shown in the table below:
| Algorithm | Minimum | Maximum | Mean Average | Std. Deviation |
|---|---|---|---|---|
| HC | -948.285209 | -110.811574 | -507.114183 | 245.121166 |
| ILS | -923.058723 | -200.301893 | -571.793068 | 191.732634 |
The boxplot for both executions is also shown in the image below:
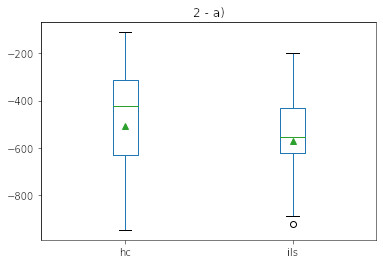
This is where ILS tends to shine brighter! The harder the problem, the better are the results. ILS tops HC in almost all aspects, specially in std deviation, which suggests less randomness than HC, and a best minimum performance by HC suggests just a bare luck in picking a specially good attraction area by randomness since the maximum and std deviation lacks so much from the ILS runs.
Configuration 2.b
This setting had the following constraints on variables:
- −511 ≤ 𝑥 ≤ 512
- -404 ≤ 𝑦 ≤ 405
Hill Climbing Parameters
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 500
- Max consecutive iterations without improvements allowed: 50
Iterated Local Search Parameters
- Perturbation size (step size): 0.5
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 50
- Local search algorithm: Hill Climbing, with:
- Noise size (step size): 0.25 for both variables
- Stop cyteria: max iterations or max consecutives iterations without improvements
- Max iterations allowed: 200
- Max consecutive iterations without improvements allowed: 2
Results and Discussion
The 30 independent individual executions results ran is shown in the table below:
| Algorithm | Minimum | Maximum | Mean Average | Std. Deviation |
|---|---|---|---|---|
| HC | -959.631515 | -959.388812 | -959.552555 | 0.067009 |
| ILS | -959.636417 | -959.517764 | -959.601634 | 0.026641 |
The boxplot for both executions is also shown in the image below:
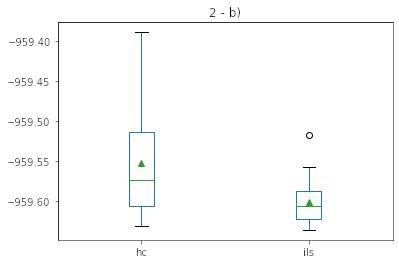
Although really near the HC results, ILS performes better in every aspects measured. It is known a smaller search space tends to prevent early convergence for both approaches, but ILS is specially better in the std. deviation results in this benchakrk, which is somehow odd since the smaller search space tends to benefit the HC algorithm as the local minimum values probability to be the global minimum one in the domain is way better. Yet again, a better std. deviation result for ILS compared to HC in this benchmark tends to show the 2.a parameters could be better tuned to favor ILS, as its way more powerful than HC alone but yet has closer or even worse results depending on the way you see it.